INSTITUTO BASICO ANIBAL ALBUREZ ROCA
MUNICIPIO DE SAN MARTÍN JILOTEPEQUE
DEPARTAMENTO DE CHIMALTENANGO
GUATEMALA
PRIMERA UNIDAD
- TEORIA DE CONJUNTO
- UNIÓN DE CONJUNTO
- INTERSECCIÓN DE CONJUNTO-
CONJUNTO
Es una agrupación, clase o colección de objetos denominados
elementos del conjunto (aunque cualquier definición dada esconde implícitamente paradojas lógicas o contradicciones).
Por objeto entenderemos no sólo entes físicos, como mesas, sillas, etc., sino también entes abstractos, como son números, letras, etc. La
relación de pertenencia entre los elementos y los conjuntos siempre es perfectamente discernible, en otras palabras, si un objeto pertenece a un conjunto o no, siempre puede calificarse como verdadero o falso .os conjuntos son uno de los conceptos básicos de la matematica Como ya se ha dicho, un conjunto es, más o menos, una colección de objetos, denominados
elementos. La notación estándar utiliza llaves
{, y
} alrededor de la lista de elementos para indicar el contenido del conjunto, como por ejemplo:
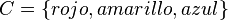
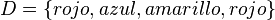

Las tres líneas anteriores denotan el mismo conjunto. Como puede verse, es posible describir el mismo conjunto de diferentes maneras: Bien dando un listado de sus elementos (lo mejor para conjuntos finitos pequeños) o bien dando una propiedad que defina todos sus elementos. Por otro lado, no importa el orden, ni cuantas veces aparezcan en la lista sus elementos.
Si A y B son dos conjuntos y todo elemento x de A está contenido también en B, entonces se dice que A es un subconjunto de B. Todo conjunto tiene como subconjunto a sí mismo y al conjunto vacío, {}.
La unión de una colección de conjuntos:  es el conjunto de todos los elementos contenidos en, al menos, uno de los conjuntos
es el conjunto de todos los elementos contenidos en, al menos, uno de los conjuntos  y se representa:
y se representa: 
La intersección de una colección de conjuntos:  , es el conjunto de todos los elementos contenidos en todos los conjuntos:
, es el conjunto de todos los elementos contenidos en todos los conjuntos:  y se representa:
y se representa: 
los conjuntos también son nombrados según el número de elementos que tengan ejemplo conjunto vacío, conjunto unitario,conjunto finito,conjunto infinito. Algunos ejemplos de conjuntos de números son:
- Los números naturales utilizados para contar los elementos de un conjunto.
- Los números enteros
- Los números racionales
- Los números reales, que incluyen a los números irracionales
- Los números complejos que proporcionan soluciones a ecuaciones del tipo: x2 + 1 = 0.
La teoría estadística se construye sobre la base de la teoría de conjuntos y la teoría de la probabilidad.
Los conjuntos son uno de los conceptos básicos de las matematícas. Como ya se ha dicho, un conjunto es, más o menos, una colección de objetos, denominados
elementos. La notación estándar utiliza llaves
{, y
} alrededor de la lista de elementos para indicar el contenido del conjunto, como por ejemplo:
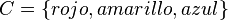
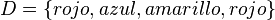

|
|
|
|
|
|
Relaciones entre conjuntos |
|
Las tres líneas anteriores denotan el mismo conjunto. Como puede verse, es posible describir el mismo conjunto de diferentes maneras: Bien dando un listado de sus elementos (lo mejor para conjuntos finitos pequeños) o bien dando una propiedad que defina todos sus elementos. Por otro lado, no importa el orden, ni cuantas veces aparezcan en la lista sus elementos.
Si A y B son dos conjuntos y todo elemento x de A está contenido también en B, entonces se dice que A es un subconjunto de B. Todo conjunto tiene como subconjunto a sí mismo y al conjunto vacío, {}.
La unión de una colección de conjuntos:  es el conjunto de todos los elementos contenidos en, al menos, uno de los conjuntos
es el conjunto de todos los elementos contenidos en, al menos, uno de los conjuntos  y se representa:
y se representa: 
La intersección de una colección de conjuntos:  , es el conjunto de todos los elementos contenidos en todos los conjuntos:
, es el conjunto de todos los elementos contenidos en todos los conjuntos:  y se representa:
y se representa: 
los conjuntos también son nombrados según el número de elementos que tengan ejemplo conjunto vacío, conjunto unitario,conjunto finito,conjunto infinito. Algunos ejemplos de conjuntos de números son
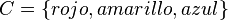
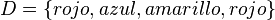

 es el conjunto de todos los elementos contenidos en, al menos, uno de los conjuntos
es el conjunto de todos los elementos contenidos en, al menos, uno de los conjuntos  y se representa:
y se representa: 
 , es el conjunto de todos los elementos contenidos en todos los conjuntos:
, es el conjunto de todos los elementos contenidos en todos los conjuntos:  y se representa:
y se representa: 


